Yapısal Eşitlik Modellemesi (SEM), istatistiksel bir analiz yöntemi olup, birçok bilim dalında karmaşık ilişkileri modellemek ve incelemek için kullanılır. Özellikle sosyal bilimler, ekonomi, psikoloji ve pazarlama alanlarında yaygın olarak kullanılan bu yöntem, değişkenler arasındaki karmaşık ilişkileri anlamamıza ve tahminler yapmamıza olanak tanır. Bu makalede, SEM’nin temel kavramlarını ve Amos yazılımını kullanarak nasıl gerçekleştirildiğini inceleyeceğiz.
Yapısal Eşitlik Modellemesi Nedir?
Yapısal Eşitlik Modellemesi (SEM), birden fazla değişken arasındaki ilişkileri aynı anda modellemek için kullanılan bir istatistiksel analiz yöntemidir. SEM, gözlemlediğiniz değişkenlerin birbirleriyle nasıl ilişkili olduğunu, hangi değişkenlerin diğerlerini etkilediğini ve bu ilişkilerin karmaşıklığını incelemenize yardımcı olur.
SEM, bir dizi temel bileşeni içerir:
- Ölçüm Modeli (Measurement Model): SEM’nin başlangıç noktası, değişkenlerin nasıl ölçüldüğünü ve hangi faktörler tarafından temsil edildiğini belirlemektir. Bu, değişkenlerin bir araya gelerek faktörleri oluşturduğu yapısını ortaya koyar.
- Yapısal Model (Structural Model): Yapısal model, faktörler arasındaki ilişkileri ve değişkenlerin bu faktörlere nasıl katkıda bulunduğunu gösterir. Bu, modelin ana bölümüdür ve karmaşık ilişkileri açıklar.
SEM, bu iki temel bileşeni bir araya getirir ve bir modelin yapısını ve ilişkilerini analiz etmeye olanak tanır. Sonuç olarak, SEM ile birçok değişken arasındaki karmaşık ilişkileri modelleyebilir ve verilerinizi daha iyi anlayabilirsiniz.
Amos Yazılımı Nedir?
Amos, yapısal eşitlik modellemesi (SEM) ve yol modellemesi gibi birçok istatistiksel analiz yöntemini destekleyen güçlü bir analiz yazılımıdır. Amos, bu tür analizleri kolayca gerçekleştirmenize ve sonuçları anlamak için görselleştirmeler sunar.
Amos’un avantajları şunlar olabilir:
- Grafiksel Kullanıcı Arayüzü: Amos, kullanıcı dostu bir grafik arayüzüne sahiptir, bu da analizlerinizi görsel olarak tasarlayabilmenizi ve düzenleyebilmenizi sağlar.
- Yapısal Eşitlik Modellemesi (SEM): Amos, karmaşık yapısal eşitlik modellerini kolayca oluşturmanıza olanak tanır. Bu, değişkenler arasındaki ilişkileri daha iyi anlamanıza yardımcı olur.
- Model Uygunluk İstatistikleri: Amos, modelinizin verilere ne kadar iyi uyduğunu değerlendirmenize yardımcı olan çeşitli uygunluk istatistikleri sunar.
Amos ile Yapısal Eşitlik Modellemesi Yapmak
Amos kullanarak SEM yapmak oldukça basittir. İşte temel adımlar:
Adım 1: Veri Hazırlığı
Her analizde olduğu gibi, SEM için de doğru verilere ihtiyaç vardır. İlk olarak, verilerinizi temizleyin ve gerektiğinde dönüştürün.
Adım 2: Ölçüm Modeli Oluşturma
Amos ile ölçüm modelinizi oluşturun. Bu, hangi değişkenlerin hangi faktörleri temsil ettiğini ve bu faktörlerin nasıl ölçüldüğünü belirler.
Adım 3: Yapısal Modeli Oluşturma
Yapısal modeli oluşturun. Bu, faktörler arasındaki ilişkileri ve değişkenlerin bu faktörlere nasıl katkıda bulunduğunu açıklar.
Adım 4: Modeli Tahmin Etme
Modelinizi oluşturduktan sonra, Amos size istatistiksel sonuçları sunacaktır. Bu sonuçlar, modelin uygunluğunu, faktörlerin etkilerini ve ilişkileri değerlendirmenize yardımcı olur.
Adım 5: Sonuçları Değerlendirme
Sonuçları dikkatlice değerlendirin ve modelinizi yorumlayın. Hangi faktörlerin hangi değişkenlerle ilişkili olduğunu ve bu ilişkilerin istatistiksel olarak anlamlı olup olmadığını kontrol edin.
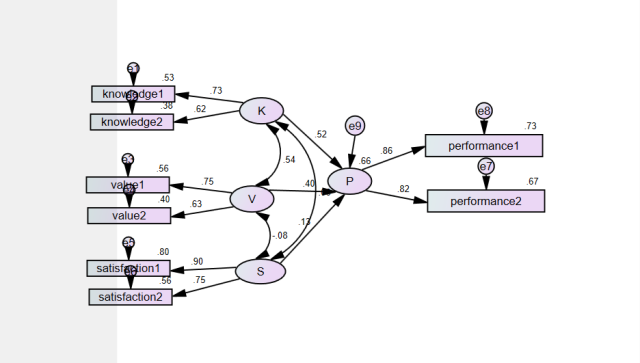
Amos ile Yapısal Eşitlik Modellemesi Sonuçları
Amos yazılımı ile gerçekleştirilen yapısal eşitlik modellemesi sonuçları, karmaşık veri yapılarının ve değişkenler arasındaki ilişkilerin analiz edilmesini sağlar. Bu sonuçlar, analizimizin güvenilirliği, modelin uygunluğu ve her bir değişkenin diğerleri üzerindeki etkisi hakkında önemli bilgiler sunar.
Model Uygunluğu
İlk olarak, yapısal eşitlik modellemesi sonuçlarını değerlendirmek için model uygunluğu istatistiklerine göz atalım:
- Kök Ortalama Kare Hata (RMSEA): RMSEA değeri, modelin uygunluğunu değerlendirmek için kullanılır. Genellikle 0 ile 1 arasında bir değer alır. RMSEA değeri ne kadar düşükse, modelin verilere o kadar iyi uyduğunu gösterir. Örneğin, RMSEA değeri 0.05 ise, modelin mükemmel uyum sağladığını gösterir.
- Ayarlanmış Uyum İndeksi (AGFI): AGFI, modelin uygunluğunu değerlendirmek için kullanılan bir başka istatistiktir. Değerler 0 ile 1 arasında değişir ve 1’e ne kadar yakınsa, modelin verilere o kadar iyi uyduğunu gösterir.
- Uyum İndeksi (CFI): CFI, modelin uygunluğunu değerlendiren bir diğer istatistiktir. CFI değeri ne kadar yüksekse, modelin verilere o kadar iyi uyduğunu gösterir.
- Chi-Kare İstatistiği (χ²): Chi-kare istatistiği, modelin verilere uygun olup olmadığını değerlendirmek için kullanılır. Bu istatistik değeri ne kadar düşükse, modelin verilere o kadar iyi uyduğunu gösterir.
Model uygunluğu istatistikleri, yapısal eşitlik modellemesi sonuçlarının verilere ne kadar iyi uyduğunu değerlendirmemize yardımcı olur. Bu istatistikler, modelin geliştirilip iyileştirilmesi gerekip gerekmediğini belirlemede önemlidir.
Değişkenler Arası İlişkiler
Yapısal eşitlik modellemesi sonuçları, değişkenler arasındaki ilişkileri değerlendirmemize olanak tanır. Her bir değişkenin faktörlerle olan ilişkisi, modelin analitik gücünü ve her bir değişkenin diğerleri üzerindeki etkisini açıklar.
Örneğin, bir müşteri sadakati modelinde, “Müşteri Memnuniyeti” faktörü ile “Ürün Kalitesi” faktörü arasındaki ilişki pozitif bir yönde olabilir. Bu, ürün kalitesinin artmasıyla müşteri memnuniyetinin de arttığını gösterir.
İstatistiksel Anlamlılık
Ayrıca, yapısal eşitlik modellemesi sonuçlarında değişkenlerin istatistiksel anlamlılığını değerlendirmelisiniz. Bu, değişkenlerin diğerleri üzerindeki etkisinin rastgele olup olmadığını belirler. İstatistiksel anlamlılık genellikle p-değeri kullanılarak değerlendirilir. p-değeri, bir değişkenin etkisinin rastgele bir farklılık olup olmadığını belirlemeye yardımcı olan istatistiksel bir değerdir.
Sonuç olarak, yapısal eşitlik modellemesi sonuçları, veri setinin karmaşıklığını ve değişkenler arasındaki ilişkileri açıklar. Model uygunluğu istatistikleri, modelin ne kadar iyi uyduğunu gösterirken, değişkenler arası ilişkiler ve istatistiksel anlamlılık, analiz sonuçlarının anlamını derinleştirir.
Veri, modern dünyanın en değerli varlıklarından biri haline gelmiştir ve iş dünyasında, araştırmada ve karar verme süreçlerinde kritik bir rol oynamaktadır. Biz, veri analizi konusundaki tutkulu bir topluluk olarak, veri biliminin ve analizinin gücünü vurguluyoruz. Web sitemiz, işletmelerden akademisyenlere ve veri meraklılarına kadar herkesin veri analizi becerilerini geliştirmesine yardımcı olmayı amaçlayan bir kaynaktır. Misyonumuz, veri analizi sürecini anlaşılır ve erişilebilir hale getirmek, verilerin içinde gizlenen değeri açığa çıkarmak ve daha bilinçli kararlar almalarını desteklemektir.
Web sitemiz, geniş bir veri analizi yelpazesi sunmaktadır. Hangi sektörde olursanız olun veya hangi veri analizi aracını kullanıyorsanız kullanın, ihtiyaçlarınıza uygun hizmetler sunuyoruz. SPSS, R, Python, Excel veya diğer analiz araçlarını kullanarak veri madenciliği, hipotez testleri, regresyon analizi, zaman serisi tahmini, segmentasyon ve daha fazlasını içeren çeşitli analiz türlerini kapsarız. Ayrıca, öğrenmeyi kolaylaştırmak için zengin kaynaklar, öğreticiler ve interaktif araçlar sunuyoruz.
Web sitemizdeki uzman ekibimiz, veri analizi konusundaki derin bilgileri ve deneyimleri ile sizin yanınızda. Kullanıcıların ihtiyaçlarını anlamak ve en iyi sonuçları elde etmelerine yardımcı olmak için buradayız. Veri analizi sürecini karmaşıklıktan arındırarak ve pratik örneklerle anlatarak size rehberlik edeceğiz. Veriye dayalı kararlarınızı daha güçlü hale getirmenize yardımcı olmak için buradayız. Siz de veri analizi dünyasına adım atmak veya mevcut becerilerinizi geliştirmek istiyorsanız, sitemizi keşfedin ve veri ile daha derinlemesine bağlantı kurun.


